Basic GMAT Math Facts and Formulas

Performing well on the quantitative section of GMAT requires a mix of math theory, test taking strategy, and critical thinking skills. While it’s important not to approach the quant section of the GMAT like a math test, it is also helpful to have logged certain facts and formulas in your brain. Most of the math theory you need to know does not go beyond high school algebra, so you’ve almost certainly “known it” before. You just need to re-learn and refresh.

In this article, we’ll review some of the basic math facts that will serve you well on the GMAT. You should NOT think that you need to remember ALL of the information in this blog article. But to the extent you understand the theory and can commit some of these facts to memory such that you can quickly recall them, you’ll save yourself time and perhaps even answer a few more questions correctly on the GMAT. This will boost your GMAT quant score.

In this article we’ll cover the following:

• Important GMAT math definitions
• Words to math translation
• Common fractions, decimals, and percents seen on the GMAT
• PEMDAS for the GMAT
• Rules about positive and negative numbers
• Prime numbers
• Powers of numbers
• Other key numbers it might be worth remembering
• Rules of divisibility on the GMAT
• Exponents and roots

In separate articles, we'll cover useful facts and formulas for GMAT geometry and trigonometry, statistics , and combinatorics on the GMAT..

Important GMAT math definitions

Positive integers = any whole number greater than 0 is a positive integer. This includes 1, 2, 3, but also 498, etc.

Negative integers = any whole number below 0. -1,-2,-3 and -498, for example.

|Absolute value |= the distance between a real number X and the origin 0. The absolute value of both 5 and -5 is 5.

Digits = 0, 1, 2, 3, 4,5,6,7,8,9

Consecutive numbers = numbers that are in order or next to each other

Reciprocal of x = 1 / x (when not equal to 0)

Product = the result of multiplication

Factor = if n = m * p, then m and p are factors of integer n

Divisor = the same as a factor

Multiple = n is a multiple of m if n / m is an integer. This means that n is always greater than or equal to m

Words to math translation on the GMAT

It is also useful to understand how words can be translated to math to answer GMAT quant problems correctly. Oftentimes we need to take a sentence and turn it into its underlying math. To do this type of work, keep in mind that:

• Is and are in math means equal = 
• Of in math means multiply *
• What in math refers to variables (x,y,z)
• Greater or less than is often denoted by > or < 
• Sum means add
• difference means subtract
• Quotient in math means divide

Common fractions, decimals, and percents seen on the GMAT

a / b + c / b = (a + c) / b

a / b * c / d = a * c / b * d

(a / b) / ( c / d) =( a * d ) / (b * c)

1 / 1 = 1.0 = 100%

1 / 2 = 0.5 = 50%

1 / 3 = .333 = 33.3%

1 / 4 = .25 = 25%

1 / 5 = .20 = 20%

1 / 6 = .166 = 16.6%

1 / 7 = .143 = 14.3%

1 / 8 = 0.125 = 12.5%

1 / 9 = .111 = 11.1%

1 / 10 = .10 = 10%

PEMDAS for the GMAT

PEMDAS is an acronym that can help you remember how to solve a math expression using the correct order of operations. PEMDAs refers to PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition and Subtraction (from left to right).

Rules about positive and negative numbers on the GMAT

A positive number multiplied or divided by a positive number is always positive.

A positive number multiplied or divided by a negative number is always negative.

A negative number multiplied or divided by a positive number is always negative.

A negative number multiplied or divided by a negative number is always positive.

Prime numbers on the GMAT

It can be helpful to know about prime numbers on the GMAT. As a reminder, a prime number is a whole number greater than 1 that has only two factors: 1 and the number itself. Therefore, prime numbers are only divisible by the number 1 and themselves.

On the GMAT, it might be helpful to familiarize yourself with prime numbers and specifically, the prime numbers through 100: 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89, and 97.

Powers of Numbers

As a reminder, a “power of a number” refers to raising a number to the 2^nd, 3^rd, or 4^th power, etc. So, 2 to the power of 2 = 2 ^2 , or 4. 2 raised to the power of 3 refers to 2 ^3 , or 2 * 2 * 2 = 8.

Here are some common powers of numbers to remember for the GMAT.

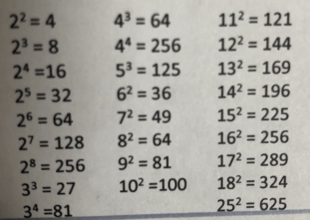
Other key numbers it might be worth remembering to score well on the GMAT

While the GMAT is a test of critical thinking and logic, it can be helpful to simply remember some facts and figures instead of having to work out the math. Below are some numbers it might just be useful to remember. In thinking about these numbers, the following definitions are useful to keep in mind:

A root of a number, x, is a different number which when you multiple that number by itself a given number of times, equals X. The second root is usually called a “square root” and the third root is called a cube root. Examples usually help. The second root of 4 = 2, because 2 * 2 = 4. The third root of 8 is also 2, because 2 * 2 * 2 = 8. Or, when you multiple 2 by itself three times, you get 8.

A factorial is the product of any given integer and all the integers before it. It is written using an exclamation point. So “four factorial” is written 4! and equals 4 x 3 x 2 x 1 or 24.

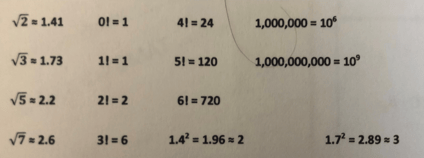
Rules of divisibility on the GMAT

Often when you are working out GMAT quant problems, you need to know if you can easily divide one number into another. Here are some useful GMAT divisibility rules:

• A number is divisible by 2 if the last digit is divisible by 2
• A number is divisible by 4 if the last two digits are divisible by 4
• A number is divisible by 8 if the last three digits are divisible by 8
• A number is divisible by 3 if the sum of all the digits is divisible by 3
• A number is divisible by 9 if the sum of all the digits is divisible by 9
• A number is divisible by 5 if the last digit is 5 or 0

Exponents and Roots on the GMAT

When you are dealing with GMAT quant problems that involved exponents and roots, a failure to recall simple rules of adding, subtracting, multiplying, or dividing using exponents and roots can be debilitating. Here are some of the most important rules to keep in mind.

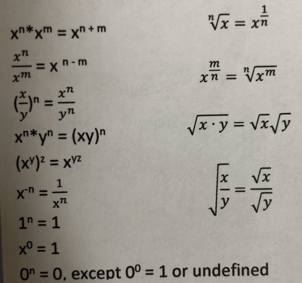
Summary of Math Facts and Formulas for the GMAT

Again, you do NOT need to remember all of the above information. But the topics and the theory should be familiar to you, and some of it could and should be committed to memory. It a future article we’ll cover some of the geometry and trigonometry rules and relationships that are helpful to know when you take the GMAT.