While much of the subject matter on the Quant section of the GRE will be familiar to you, one common question type is likely to be unfamiliar: Quantitative Comparisons....
The GRE’s Quantitative section doesn’t test particularly advanced math, but it does demand that you apply a variety of fundamental concepts in many novel ways.
What really makes the Quant section difficult is that you have to constantly figure out how to get from point A to point B. You might find yourself going, “Alright I know I have to use y = mx + b here, but how am I supposed to find the y-intercept given this information?”
Devising the steps you’ll need to solve a problem can be particularly difficult on the Quantitative Comparison questions. These are the ones where you have to decide which of two quantities is greater, instead of simply solving a problem and selecting the answer choice that matches your own answer.
The answer choices for these problems are always:
- Quantity A is greater.
- Quantity B is greater.
- The two quantities are equal.
- The relationship cannot be determined from the information given.
It may seem like these questions require a higher-level, abstract understanding of the math concept being tested, but the good news is that trying some actual numbers works just fine.
The Big Secret? Try Actual Numbers
Quantitative Comparison questions are almost always algebra questions. Remember that for any algebraic equation, expression, or system to work, you need to be able to use actual numbers in it. This strategy is known as plugging in.
So why not try some? Let’s take a look at this strategy in action.
Here we have about as simple of a Quantitative Comparison problem as it gets. This one has just two algebraic expressions. Choosing a value for x will make it easy to determine which one is greater.
Let’s say x = 5.
Substituting that value into Quantity A, we’d get 52+ 1, or 26.
Substituting that value into Quantity B, we’d get 2 (5) – 1, or 9.
Ok, it’s looking like Quantity A is greater, but it’s always a good idea to test a second value. Try one that is as different as possible from the one we initially chose.
Since we want something pretty much opposite, let’s try a negative number, x = –10.
Quantity A would become (–10)2+ 1, or 101.
Quantity B would become 2 (–10) – 1, or –21.
Quantity A is still greater, so we’ll choose answer choice A.
A Step-by Step Strategy for Quantitative Comparison
The most formulaic approach is the best one for Quantitative Comparison questions. If you have a good way to test the given quantities rigorously, why not use it over and over and over again? Here’s a step-by-step strategy that will always work.
- Read over Quantity A and Quantity B and decide if there are any specific rules or formulas you’ll need.
- Plug in the same number to each quantity. If it seems like it’s important to figure out if a quantity will be positive or negative, try a negative number. If you think you want to push the quantity to an extreme, try a really big number.
- Plug in another, very different number to each quantity. If you chose a negative number the first time, try a positive one now. If you tried a huge number last time, try a fraction.
- Did you get a different relationship between the two quantities after each round of plugging in a number? Then you likely can’t determine which quantity is greater, and answer choice D is starting to look pretty good. Take a moment to think about any other numbers you might want to test here, but don’t spend all day on it. It’s totally ok to select answer choice D!
Let’s try that strategy again.
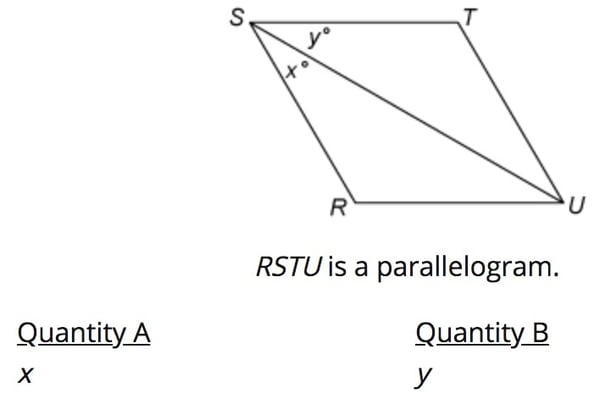
Step 1. Here we have a parallelogram. This polygon has 4 sides, so using the formula 180(n – 2), with n representing the number of sides, we can determine that the sum of all of the angles in this parallelogram is 360º.
Step 2. Since xº and yº add up to an acute angle, we’ll choose an acute value. So we’ll say that x + y = 80.
Now let’s choose some values. Let’s say x = 70. Well, if that’s the case, then y = 10.
Step 3. Ok well, what if x was much smaller. Let’s say x = 20. In that case y = 60.
Step 4. It seems like we can’t really decide which one is larger. In fact, they could be equal to each other for all we know, with x = 40 and y = 40.
Therefore, we’ll choose answer choice D.
Incorporate this step by step process into your study time and you'll almost certainly see positive results. When you take a methodical approach, Quantitative Comparison questions don't seem as daunting, and you'll be well on your way to increasing that Quant score!