Let’s look at three math concepts that are very helpful on the GRE’s Quantitative Reasoning sections. Each concept involves triangles. The first concept, triangle...
The Quantitative Reasoning section of the GRE measures your basic mathematical skills, as well as your understanding of basic mathematical concepts pertaining to arithmetic, algebra, geometry, and data analysis. Furthermore, the Quantitative Reasoning section measures your ability to reason mathematically, and to solve mathematical problems based on analyzing and evaluating information presented to you in the problem.
Now that you know what to expect on the GRE Quantitative section, you shouldn’t panic about the content that you‘ll encounter; you have seen this material before. Remember, the problems you see in this section are based on a high school math and statistics course, which you’ve probably already taken if you are preparing for the GRE exam. So, how can you score well on the GRE Quantitative section? Reviewing basic mathematical formulas, rules, and equations should be your starting point. In this series of blog articles, we’ll review basic formulas, rules, and concepts for arithmetics, algebra, geometry, and data analysis you should be familiar with in order to tackle the GRE Quantitative section. We’ll also review strategies to tackle these questions, as well as a practice problem so that you can see how to apply the strategy.
In this blog article, we’ll be focusing on geometry formulas, rules, concepts, as well as the kinds of geometry problems you should expect to see on the GRE Quantitative exam. In the next blog article, we will discuss strategies on how to approach GRE Geometry questions, as well as solve some practice problem so that you have an understanding of how to apply the strategies.
GRE GEOMETRY DIGEST
As mentioned earlier, geometry is one of the four math subjects that you will be tested on in the GRE exam. Most of the GRE Geometry problems are centered on parallel and perpendicular lines, circles, triangles, quadrilaterals, other polygons, congruent and similar figures, three-dimensional figures, area, perimeter, volume, the Pythagorean theorem, and angle measurement in degrees. That’s a lot! So how can you know what to do to correctly interpret, analyze, and solve a geometry problem? First, you should familiarize yourself with all of the basic geometry formulas and rules.
Lines and Angles
When two lines intersect at a point, they form four angles, each of which has the same vertex.
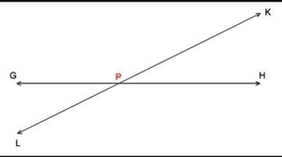In the figure, the two lines that are shown are line LK, and line HG, and the vertex, or where the lines intersect, is point P. Angles KPH and GPL are called opposite angles. Opposite angles have equal measures, thus making them congruent angles.
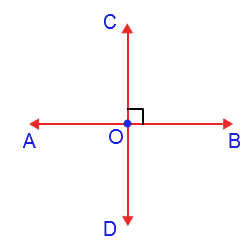Lines that intersect and form four congruent angles are called perpendicular lines. Each of the four angles are 90 degrees. Angles that are 90 degrees are called right angles. The small square at the vertex of the perpendicular lines indicates that the angle is a 90 degree angle.
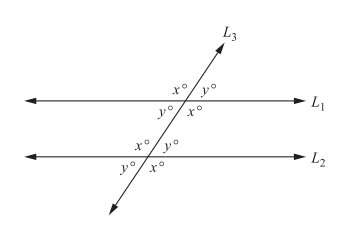Two lines that don’t intersect are called parallel lines. The adjacent figure shows two parallel lines, l1 and l2, that are intersected by a third line, l3, forming eight angles. Note that all the x angles are all congruent angles, thus they all have the same degree measure. All the y angles are also congruent angles and have the same degree measure. Another thing to note is that when you add angle x and angle y, they total 180 degrees.
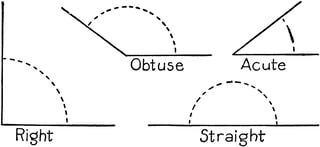
An angle that measures less than 90 degrees is called an acute angle. An angle that measures more than 90 degrees is called an obtuse angle. An angle that measures 180 degrees is called a straight angle.
Polygons
A polygon is a shape with three or more sides. Each corner where two sides meet is called a vertex. Included below is a diagram illustrating different kinds of polygons.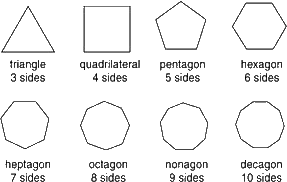
Note that the triangle is the simplest polygon, and that you can divide polygons with more than three sides into triangles. A quadrilateral (4 sides) can be divided into 2 triangles. A pentagon (5 sides) can be divided into 3 triangles. A hexagon (6 sides) can be divided into 4 triangles. Or, in other words, a polygon with n sides can be divided into (n-2) triangles.
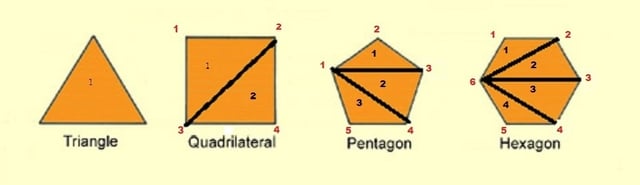
To determine the sum of the measure of each interior angle of an n-sided polygon, you can use the following equation: (n-2)*(180). For example, the sum of interior angles in a quadrilateral is (n=4) → (4-2)*(180) = 360 degrees. The sum of interior angles in a decagon is (n=10) → (10-2)*(180) = 1440 degrees.
A polygon in which all of the sides and all of the angles are congruent is called a regular polygon. The perimeter of a polygon is the sum total of the lengths of its sides. The area of a polygon refers to the area of the region enclosed by the polygon.
Triangles
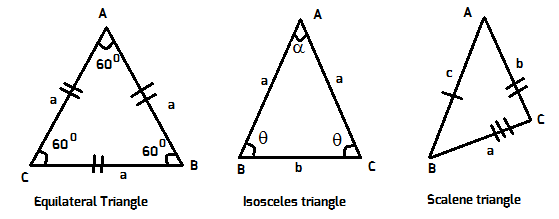
Every triangle has three sides, and three angles which add up to 180 degrees.
An equilateral triangle is a triangle in which all three angles of the triangle are equal. In other words, all three angles are 60 degrees.
An isosceles triangle is a triangle in which two of the three angles of the triangle are equal.
A scalene triangle is a triangle in which none of the angles are equal to each other.
In any triangle, the longest side is always directly opposite the largest angle. Take for instance the hypotenuse of a triangle; the hypotenuse is the longest side of a triangle and is always opposite the largest angle in a triangle. In the image below, the hypotenuse is opposite a right angle (the largest angle).
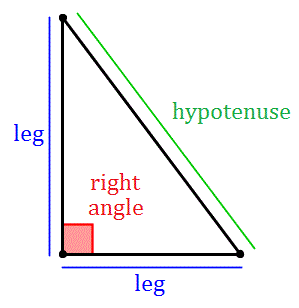
The same logic applies for small sides; the smallest side is always directly opposite the smallest angle.
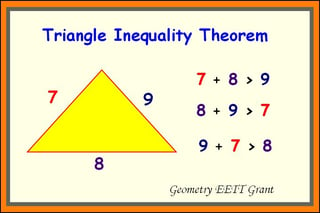
The triangle inequality rule is a rule that you’ll surely encounter on the GRE math section. The rule states that the length of one side of a triangle is less than the sum of the lengths of the other two sides and greater than the difference of the lengths of the other two sides.
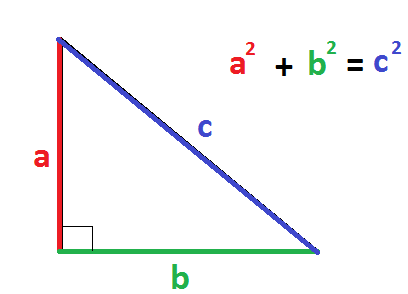
The Pythagorean Theorem is a rule that applies only to right angle triangles. The rule states that the square of the hypotenuse is equal to the sum of the squares of the other two legs. That is c2=a2 + b2 where c is always the hypotenuse, and a and b are always the lengths of the other two legs of the triangle.
Quadrilaterals
Quadrilaterals are four-sided figures with four angles that add up to 360 degrees. In other words, squares, rectangles, and parallelograms are all quadrilaterals.
To find the perimeter of a quadrilateral, simply add up the lengths of all four sides. To find the area of a quadrilateral, multiply its width by its length. (To find the area of a parallelogram, make sure to multiply the base by the height of the figure, and not by the side length).
Circles
Circles come up pretty often on the GRE Math section. Here’s what you need to know about circles:
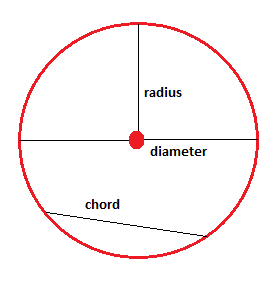
A chord a line that connects to points on the circumference of a circle. The radius is a line that extends from the center of a circle to a point on the circumference of a circle. The diameter is a line that connects two points on the circumference of a circle and also passes through the center of the circle. Thus, the diameter is both a chord and twice the length of the radius. The radius is not a chord.
The circumference of a circle is simply the perimeter of a circle, or the distance around a circle. To find the circumference of a circle use the following formula: circumference = 2r𝚷 or d𝚷 where r is the radius and d is the diameter. The formula to find the area of a circle is area =𝚷r2
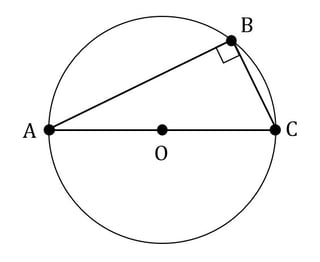
One thing that the GRE test writers like to do is inscribe objects within another object. For example, you might encounter a triangle inscribed in a circle, or a circle inscribed in a polygon, or a circle inscribed another circle (aka concentric circles). There are a couple of things you should know about inscribed figures:
- The area of a figure inscribed within another figure will not exceed the area of the surrounding figure.
- If a right triangle is inscribed within a circle, the hypotenuse of the triangle is equal to the diameter of a circle.
Now that you have refamiliarized yourself with the basic geometry formulas and rules, you are all set to tackle the Math section of the GRE. The key to correctly answering the questions on the GRE Math section involves drawing connections between the geometry question and the fundamental geometry concepts and formulas you’ve just reviewed. The more connections you are able to draw, the better shape you’ll be in to correctly solve the question. In the next blog post, we’ll focus on answering a few geometry questions by drawing connections to the fundamental geometry principles you’ve just reviewed. For more Geometry review and practice problems, PrepScholar has some great resources as well. Check it out!