One of the most important question types on the quantitative section of the GRE is Data Interpretation, which is sometimes referred to as Data Analysis. Unlike, say, the...
While you may be taking the GRE to get into graduate school, it may relieve you to know you won’t have to use math that you’ve learned past your sophomore or junior year of high school. Long-winded and drawn out problem solving and arithmetic is not the style of the GRE. So what’s the catch? If the math is so easy, why are you even reading this article on how to tackle the math section? The challenge behind this section draws from the way these limited mathematical concepts are presented to you. In a sense, you need to often systematically deconstruct the problem in the way it’s presented, to determine what is really being asked of you. Once you are able to determine what the question is asking, the actual “number-crunching” or math involved is much less than you might think.
As per ETS, here are the main points the exam is essentially assessing:- basic mathematical skills
- understanding of elementary mathematical concepts
- ability to reason quantitatively and to model and solve problems with quantitative methods
They will use the following subject matter to test your ability to successfully demonstrate competency in the above: basic shape properties (triangles, circles, quadrilaterals, etc.), exponents, integer properties, word problems.
Our friends at Magoosh have built this frequency distribution to provide better insight into the types of questions asked and how high or low yield they are:
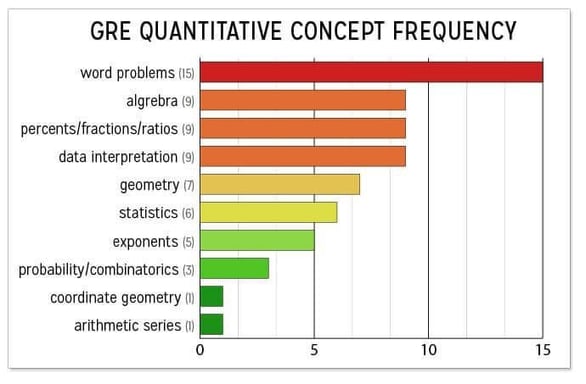
The GRE quantitative section is broken up into quantitative comparison (QC) questions and problem solving questions. The QC questions involve comparing two columns and deciding if one is greater than the other, if they are both equal or if it cannot be determined. The Problem solving section entails multiple choice and free response.
The lack of advanced math concepts on this exam provides students with a unique advantage. By getting enough practice and familiarity with the types of questions on the GRE, especially by taking as many practice exams as possible, a student has a high likelihood of success since the math concepts themselves are not terribly difficult and can be strengthened. Repeated exposure will be the best tool against some of the more seemingly tricky questions on the GRE. This is why one’s best friend during test prep is taking practice exams and going over the answers (with your tutors)! Make sure to always challenge yourself and stay consistent. Come test day, your hard work will surely pay off!
The following is an example of a math problem that may seem complicated, but only involves simple trig concepts of a 30-60-90 triangle:
What is the area of an equilateral triangle whose inscribed circle has a radius of 2?
- 12
- 16
- 12 sq rt._/3
- 16 sq rt._/3
- 4(3+2 sq rt._/2)
To begin, draw an equilateral triangle with a circle inscribed inside.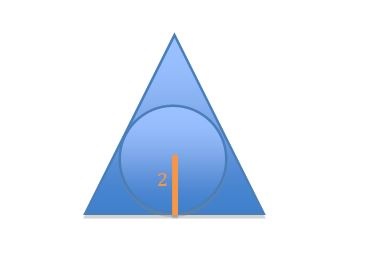
From here, you can draw a hypotenuse for a 30-60-90 right triangle from the center of the circle to either of the bottom two sides.
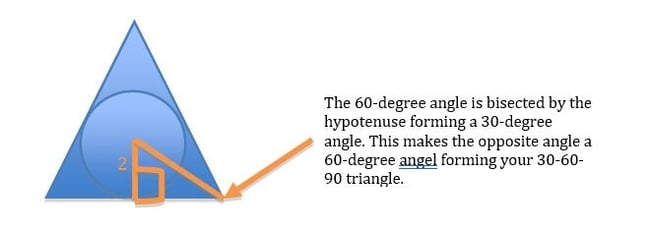
Remember that in a 30-60-90 triangle the proportions are:
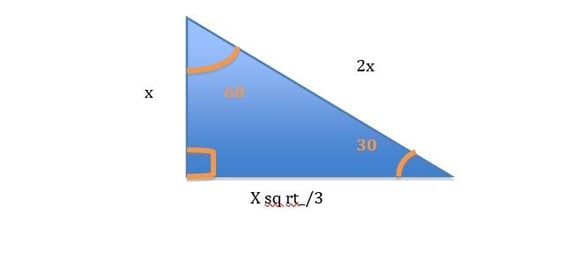
So it follows that our triangle’s sides are:
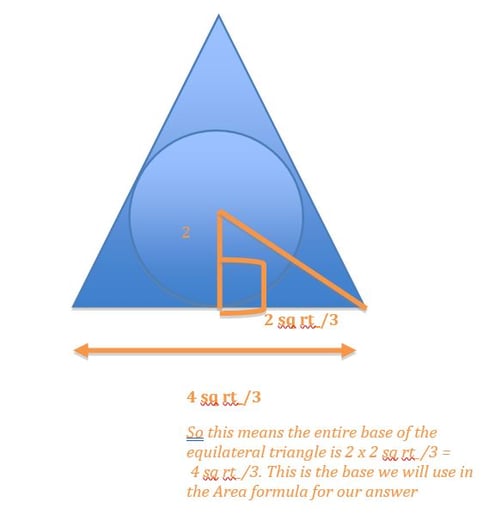
Now draw the altitude in for the big, equilateral triangle to find the height. Drawing in this altitude will allow you to form a bigger 30-60-90 right triangle.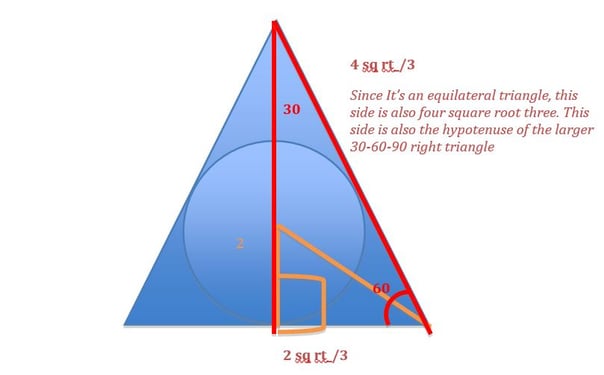
Using the same proportions of a 30-60-90 triangle we get the following side lengths of the larger triangle.
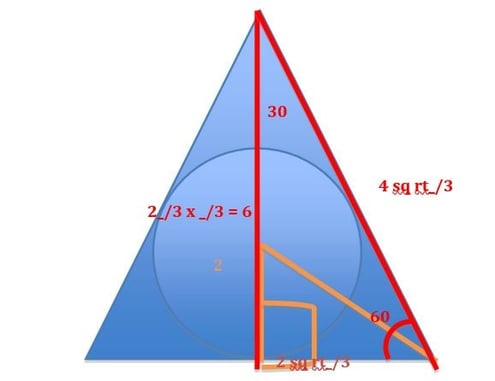
Now you can simply use the formula to calculate the area of a triangle:
Area of a Triangle = ½ (base) x (height)
= ½ (4 sq rt_/3)(6)
=24 sq rt_/3 x ½
=12 sq rt_/3
The answer is C!
Remember to first draw a picture and remember that they will simply test basic trig and math concepts, dressed up in seemingly tricky problems! Good luck!