GMAT Question of the Day #114 - VIC (variables in choices)

This blog post relates to question #114 from the Official Guide for GMAT Review, 2017.

This is a classic combined rate problem with a VIC (variables in choices) twist. The authors of the OG provide the straightforward algebraic solution, and, with the proper background in rates problems like this, you shouldn’t have any trouble understanding what they’re up to. However, VIC problems with only one or two variables are begging to be back-solved.

Start by noticing that x > y because x is the amount of time it takes to make the 800 nails when the machines work together, and y is the amount of time it takes Machine A working alone. Based on that, let’s pick x = 2 and y = 4.

Small numbers that divide 800 are going to be good picks. You might want to try some different numbers on your own. In this case I’ve set it up so that Machines A and B will work at the same rate – they work twice as fast together.

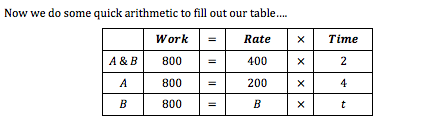
Because combined rates are always to sum of the individual rates, we know that . So, the rate of Machine B must be 200 nails per hour. Consequently, Now we plug in our picks, and . To find our target number – 4.

Takeaways:

1. When you have a VIC problem with only one or two variables, you should always consider back-solving.
2. Pay attention to the context of the problem when making your picks.
3. Also, notice that when I plugged in my picks to find my target, there was no need to actually do the computation – (A) and (B) are less than one, (C) isn’t an integer, (D) is negative, so (E), whatever it turns out to be, must be the answer
4. One last thing: the people at GMAC know that this is an efficient way to solve this problem. That’s probably why E is the correct answer. Next time you back-solve, start with (E)

 John is a Senior MyGuru GMAT tutor based in Chicago, but is also the founder of Owl Test Prep . We encourage you to check out their web-site and YouTube channel.